Plane Through Parabolic Solid of Revolution
Several previous posts examined properties of the curves produced when a cutting plane passes through a right cone at an angle (to produce a section whose edge describes a parabola or ellipse.)
A right cone can be thought of as a Solid of Revolution (SOR), produced by revolving the appropriate straight line around an axis. For example, the following image shows a portion of the graph for the equation y = 100 - 2*x revolved around the y-axis:
When this line is revolved around the y-axis, the familiar right cone is produced, through which a cutting plane can be passed to produce one of the familiar conics (parabola, circle, ellipse, and hyperbola.)
I would now like to generalize this examination by extending the concept to SORs produced by revolving non- straight lines around the y-axis. In other words, I will examine the shapes produced when a cutting plane passes through a body whose body has a circular cross-section perpendicular to the axis of revolution--but is not a right cone.
For the present example, an SOR is examined that has been produced by revolving a parabolic line around the y-axis. The line is described by
y = [1/(4c)] x^2, where c = 0.143823832162.
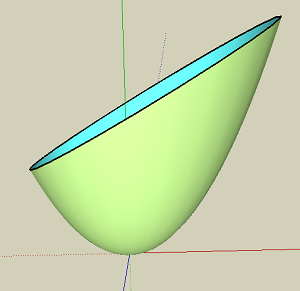
The SOR produced is shown in the following image (it may appear upside down compared to other images, but the orientation doesn't matter; the same shape is produced, which is all that is important for the sake of this investigation):
Passing a cutting plane through it,
And with the top section removed to see the resulting plane:
Looking at a cross-section (through the mid-point) of the paraboloid from the side, note a few basic features:
The origin of the coordinate system of the 2-D parabola that was used to create the paraboloid coincides with the vertex of the parabola:
positive X is to the right;
positive Y is up, and also acts as the axis of revolution, becoming the axis of the paraboloid; and
positive Z is coming out of the page toward the reader.
α is the angle at which the cutting plane goes through the paraboloid, with respect to the horizontal.
hc is the vertical distance from the vertex of the parabola to the point where the cutting plane intersects the axis of revolution. At this point, rc is the radius of the paraboloid.
ru is the distance from the axis of revolution to the upper edge of the paraboloid, measured along the inclined plane.
rl is the distance from the axis of revolution to the lower edge of the paraboloid, measured along the inclined plane.
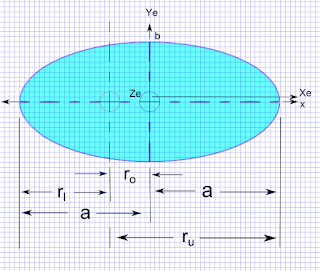
Affix a new coordinate system to the plane (xe, ye, ze). Looking at the section from above, and perpendicular to, the plane of the section, it appears as illustrated in the following image:
Positive xe is along the plane to the right, measured from the mid-point of the plane;
positive ye is up along the plane, measured from the mid-point of the plane; and
positive ze is perpendicular to the plane, coming out of the page toward the reader.
Now to calculate some of these parameters.
rl must satisfy two conditions (imposed by the original parabola):
rl cos(α) = x AND hc - rl sin(α) = y = (1/(4c)) x2. Solving these equations yields
Similarly, ru must satisfy two conditions:
ru cos(α) = x AND hc + ru sin(α) = y = (1/(4c)) x2. Solving these equations yields
If the entire length across the middle of the plane is 2a = ru + rl, then half the length is a = (ru + rl)/2:
This mid-point of the plane is offset from the axis of revolution by a distance ro measured along the plane. This parameter can be found either as ru - a or a - rl; they yield the same result:
Note that ro is independent of hc; it is a function of c and α only.
If the condition that a = 1 is imposed, expressions for c and hc in terms of each other can be derived, as well as a modified expression for ro:
The coordinate system on the cutting plane will now be used to compute some points.
Say we go along the plane a distance xe from the mid-point of the plane. At this height, the circular cross-section of the paraboloid will have a radius, rxe.
This point must satisfy the equation hc + (ro + xe) sin(α) = y = (1/(4c)) x2. So,
Also at this point, the horizontal displacement from the axis of revolution is x:
In the circular cross-section of the paraboloid this point represents an angle of
Finally, the ye along the plane is found as
Now to create a numeric example to plot the shape of the plane. Say
hc = 0.431235852853
α = 0.904556894307 radians.
Then,
a = 1
ro = 0.592028088783
Computing the ye values for several xe values, the following table is produced:
A plot of this data indicates that the plane is an ellipse. In fact, plugging each of the data points into the standard equation for an ellipse
where b is taken to be the mid-point of the section, confirms that the cutting plane is, indeed, an ellipse. The b point is found as
and the eccentricity of the ellipse is
Note that e is independent of hc and c; it is a function of α only.
In the present example, the eccentricity, e, of the ellipse is e = 0.786151377767.
A right cone can be thought of as a Solid of Revolution (SOR), produced by revolving the appropriate straight line around an axis. For example, the following image shows a portion of the graph for the equation y = 100 - 2*x revolved around the y-axis:
When this line is revolved around the y-axis, the familiar right cone is produced, through which a cutting plane can be passed to produce one of the familiar conics (parabola, circle, ellipse, and hyperbola.)
I would now like to generalize this examination by extending the concept to SORs produced by revolving non- straight lines around the y-axis. In other words, I will examine the shapes produced when a cutting plane passes through a body whose body has a circular cross-section perpendicular to the axis of revolution--but is not a right cone.
For the present example, an SOR is examined that has been produced by revolving a parabolic line around the y-axis. The line is described by
y = [1/(4c)] x^2, where c = 0.143823832162.
The SOR produced is shown in the following image (it may appear upside down compared to other images, but the orientation doesn't matter; the same shape is produced, which is all that is important for the sake of this investigation):
Passing a cutting plane through it,
And with the top section removed to see the resulting plane:
Looking at a cross-section (through the mid-point) of the paraboloid from the side, note a few basic features:
The origin of the coordinate system of the 2-D parabola that was used to create the paraboloid coincides with the vertex of the parabola:
positive X is to the right;
positive Y is up, and also acts as the axis of revolution, becoming the axis of the paraboloid; and
positive Z is coming out of the page toward the reader.
α is the angle at which the cutting plane goes through the paraboloid, with respect to the horizontal.
hc is the vertical distance from the vertex of the parabola to the point where the cutting plane intersects the axis of revolution. At this point, rc is the radius of the paraboloid.
ru is the distance from the axis of revolution to the upper edge of the paraboloid, measured along the inclined plane.
rl is the distance from the axis of revolution to the lower edge of the paraboloid, measured along the inclined plane.
Affix a new coordinate system to the plane (xe, ye, ze). Looking at the section from above, and perpendicular to, the plane of the section, it appears as illustrated in the following image:
Positive xe is along the plane to the right, measured from the mid-point of the plane;
positive ye is up along the plane, measured from the mid-point of the plane; and
positive ze is perpendicular to the plane, coming out of the page toward the reader.
Now to calculate some of these parameters.
rl must satisfy two conditions (imposed by the original parabola):
rl cos(α) = x AND hc - rl sin(α) = y = (1/(4c)) x2. Solving these equations yields
Similarly, ru must satisfy two conditions:
ru cos(α) = x AND hc + ru sin(α) = y = (1/(4c)) x2. Solving these equations yields
If the entire length across the middle of the plane is 2a = ru + rl, then half the length is a = (ru + rl)/2:
This mid-point of the plane is offset from the axis of revolution by a distance ro measured along the plane. This parameter can be found either as ru - a or a - rl; they yield the same result:
Note that ro is independent of hc; it is a function of c and α only.
If the condition that a = 1 is imposed, expressions for c and hc in terms of each other can be derived, as well as a modified expression for ro:
The coordinate system on the cutting plane will now be used to compute some points.
Say we go along the plane a distance xe from the mid-point of the plane. At this height, the circular cross-section of the paraboloid will have a radius, rxe.
This point must satisfy the equation hc + (ro + xe) sin(α) = y = (1/(4c)) x2. So,
Also at this point, the horizontal displacement from the axis of revolution is x:
In the circular cross-section of the paraboloid this point represents an angle of
Finally, the ye along the plane is found as
Now to create a numeric example to plot the shape of the plane. Say
hc = 0.431235852853
α = 0.904556894307 radians.
Then,
a = 1
ro = 0.592028088783
Computing the ye values for several xe values, the following table is produced:
| xe | ye | |
| -1 | 0 | |
| -0.9 | 0.269394770065 | |
| -0.8 | 0.370820393251 | |
| -0.7 | 0.441364549706 | |
| -0.6 | 0.494427190998 | |
| -0.5 | 0.535233134658 | |
| -0.4 | 0.566437507098 | |
| -0.3 | 0.589566849675 | |
| -0.2 | 0.60554716645 | |
| -0.1 | 0.614936054508 | |
| 0.0 | 0.618033988748 | |
| 0.1 | 0.614936054509 | |
| 0.2 | 0.60554716645 | |
| 0.3 | 0.589566849674 | |
| 0.4 | 0.5664375071 | |
| 0.5 | 0.53523313466 | |
| 0.6 | 0.494427191002 | |
| 0.7 | 0.441364549705 | |
| 0.8 | 0.370820393255 | |
| 0.9 | 0.269394770066 | |
| 1 | 0 | |
A plot of this data indicates that the plane is an ellipse. In fact, plugging each of the data points into the standard equation for an ellipse
where b is taken to be the mid-point of the section, confirms that the cutting plane is, indeed, an ellipse. The b point is found as
and the eccentricity of the ellipse is
Note that e is independent of hc and c; it is a function of α only.
In the present example, the eccentricity, e, of the ellipse is e = 0.786151377767.
Labels: conic section, ellipse, elliptical section, solid of revolution