The Golden Section: Some Related Quantities
I am going to briefly detour from the present path of investigation and examine in more detail one aspect of my previous post.
In the previous post, I sought a particular elliptical section that could be used for numerical examples and further investigation. The elliptical section selected was determined as a solution of the following quartic equation:
This quartic equation could be solved by reducing it to a quadratic equation and then solving the quadratic equation.
For example, make the substitution u = γ2.
Then the equation becomes
Or the quartic equation could be solved by reducing it to a factored form
Or the quartic equation could be solved with a polynomial root-finder. Any of these approaches would find the roots of the equation--but just the roots.
However, by finding just the roots, I believe some information is lost.
So I would like to solve it by an alternative method: forming the Companion Matrix for the fourth-degree polynomial and computing its eigenvalues and eigenvectors.
The eigenvalues are the roots of the original polynomial. Plus we get the eigenvectors.
The Companion Matrix is
This matrix has four eigenvalues: two real eigenvalues and two imaginary eigenvalues.
The two real eigenvalues are +/- 1.272019649514069.
The two imaginary eigenvalues are +/- 0.7861513777574233i.
The magnitude of the real values is recognized as the square root of the Golden Section, often denoted φ and having the value (1/2)(1 + √5) = 1.6180339887498948482...
In other words, the eigenvalues of the Companion Matrix given above can be stated in terms of φ:
The associated eigenvectors can then be calculated.
For λ1 = √φ, the following system is solved to determine the associated eigenvector:
where v is a 4-element column vector and 0 is a 4-element column vector containing all zeroes.
Depending how this system is solved, the eigenvector can be stated as
or
(Numerically, these two vectors are the same.)
Now to normalize this eigenvector. If we use the first form, the magnitude is
If we use the second form, the magnitude is
Or, one more way:
Either way, this magnitude works out to a numeric value of √3.61803398874... = 1.90211303259...
So, the normalized value of the eigenvector works out to
or
These numbers are the same as the ones that were computed numerically.
So now we have exact definitions for all the elements of the eigenvectors if needed.
In the previous post, I sought a particular elliptical section that could be used for numerical examples and further investigation. The elliptical section selected was determined as a solution of the following quartic equation:
γ4 - γ2 - 1 = 0
This quartic equation could be solved by reducing it to a quadratic equation and then solving the quadratic equation.
For example, make the substitution u = γ2.
Then the equation becomes
u2 - u - 1 = 0
Or the quartic equation could be solved by reducing it to a factored form
γ4 - γ2 - 1 = (γ2 - φ)(γ2 + k) = 0
Or the quartic equation could be solved with a polynomial root-finder. Any of these approaches would find the roots of the equation--but just the roots.
However, by finding just the roots, I believe some information is lost.
So I would like to solve it by an alternative method: forming the Companion Matrix for the fourth-degree polynomial and computing its eigenvalues and eigenvectors.
The eigenvalues are the roots of the original polynomial. Plus we get the eigenvectors.
The Companion Matrix is
This matrix has four eigenvalues: two real eigenvalues and two imaginary eigenvalues.
The two real eigenvalues are +/- 1.272019649514069.
The two imaginary eigenvalues are +/- 0.7861513777574233i.
The magnitude of the real values is recognized as the square root of the Golden Section, often denoted φ and having the value (1/2)(1 + √5) = 1.6180339887498948482...
In other words, the eigenvalues of the Companion Matrix given above can be stated in terms of φ:
λ1 = √φ
λ2 = - √φ
λ3 = (1/√φ) i
λ4 = - (1/√φ) i
λ2 = - √φ
λ3 = (1/√φ) i
λ4 = - (1/√φ) i
The associated eigenvectors can then be calculated.
For λ1 = √φ, the following system is solved to determine the associated eigenvector:
where v is a 4-element column vector and 0 is a 4-element column vector containing all zeroes.
Depending how this system is solved, the eigenvector can be stated as
or
(Numerically, these two vectors are the same.)
Now to normalize this eigenvector. If we use the first form, the magnitude is
If we use the second form, the magnitude is
Or, one more way:
Either way, this magnitude works out to a numeric value of √3.61803398874... = 1.90211303259...
So, the normalized value of the eigenvector works out to
(1/1.90211303259...) v
or
0.41330423812239913
0.3249196962329062
0.668740304976422
0.5257311121191337
These numbers are the same as the ones that were computed numerically.
So now we have exact definitions for all the elements of the eigenvectors if needed.
Labels: golden mean, golden ration, golden section, phi


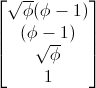




0 Comments:
Post a Comment
<< Home